Wie löse ich diese Matheaufgabe zu Kredit und Tilgung?
„Für den Kauf einer Eigentumswohnung soll ein Kredit von 200.000 Euro aufgenommen werden. Die Tilgung erfolgt in monatlichen Annuitäten bei 20 Jahren Laufzeit und einem effektiven Jahreszins von 9,38%. Wie hoch ist die monatliche Belastung für den Käufer?“
4 Antworten
Hallo risingEagle
das ist die Situation, die jeder Hauskäufer vorfindet. Das läuft nach dem folgenden Schema ab:
Die monatliche Belastung bleibt immer die gleiche.
- Im ersten Monat zahlst Du den Zins auf die 200.000€ und tilgst einen winzigen Bruchteil der Summe. Die Kreditsumme wird also ein kleinbisschen niedriger.
- Im zweiten Monat zahlst Du den Zins auf die verbleibende Kreditsumme (also ein kleinbisschen weniger Zins). Dafür erhöht sich der Betrag der Tilgung.
Und nach 20 Jahren soll die Wohnung abgezahlt sein.
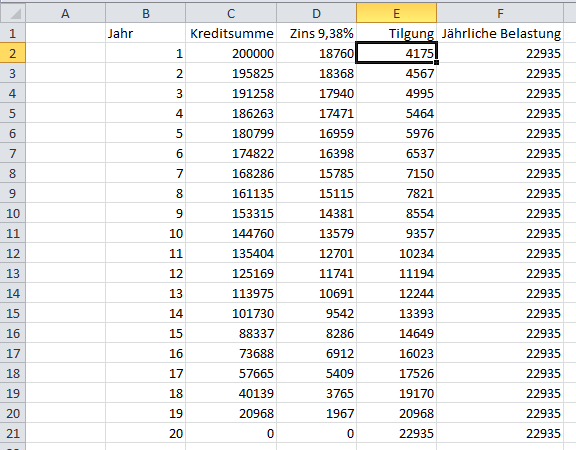
Ich hab´ das mal in Excel nachgestell, allerdings jährlich, wegen der besseren Übersicht
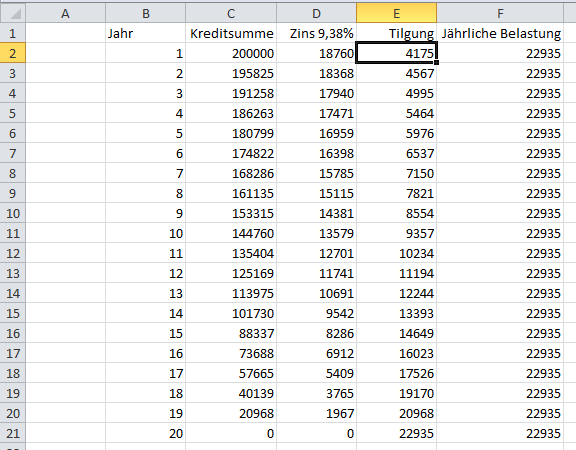
Und dabei noch einenTrick genützt. Die Tilgung habe ich automatisch mit der Zielwertsuche ermittelt.
Bei monatlicher Berechnung bist Du ein ganz klein wenig schneller mit Abzahlen fertig; bzw. die anfängliche Tilgung ist minimal geringer.
Ich hoffe, das hilft Dir. Ein Lehrer von mir sagte immer
Dumm darf man schon ein, man muss sich nur zu helfen wissen.
Excel ist eine gute Hilfe.
Gruß
Klaus
Sollte ihr das mit Stift und Papier ausrechnen? Ich würde dafür Excel zur Hilfe nehmen.
Es gibt auch online Rechner die dir das berechnen, aber ich glaube, dass will euer Lehrer nicht sehen.
Das kann man meines Wissens nur numerisch lösen (also mit einem Computer) oder annähern (irgendwelche Formeln die nur in etwa das richtige Ergebnis auswerfen)
Hast du irgendwelche Hilfsmittel?
Naja, meinen Taschenrechner halt 🤷🏼♂️
Keine Formeln nichts?
Mir ist zumindest keine bekannt 🤷🏼♂️
Hm, keine Garantie auf Richtigkeit:
200.000/12/20=x
x ist der Betrag den du monatlich im Schnitt tilgen musst um die 200k zurück zu zahlen.
200.000*0,0938=y
y sind die Zinsen die du im ersten Jahr zahlen musst. Da am Anfang des Kredites dir Zinslast höher ist, als am Ende (logisch denn am Anfang schuldest du der Bank ja mehr Geld als gegen Ende) müsste die jährliche Zinslast y in 20 Jahren linear auf 0€ sinken. Soll heißen, wenn wir die Hälfte von y nehmen, dann haben wir die durchschnittliche Zinslast pro Jahr.
Also y/2 musst du dann noch Mal durch 12 Monate teilen, da du ja die durchschnittliche Zinslast pro Monat ermitteln möchtest.
Also x+(y/2)/12= mtl Rate
Das ergebnis ist auch nur eine Näherung. Das ganze kannst du auch noch auf Monate runter brechen, dann ist es exakt ... Ist dann aber ein bisschen schwerer zu rechnen.
Zuerst den effektiven Jahreszins umwandeln in einen äquivalenten monatszins.
Und dann mit der Rentenbarwertformel die monatliche Annuität ausrechnen.
Wie rechne ich das in den Monatszins um? Mit 1,0938 hoch (1/12) und dann minus 1?
......
Aber wenn ich vom Jahreszins auf den Monatszins schließen möchte, muss ich doch den Jahreszinsfaktor hoch 1/12 nehmen und dann 1 abziehen oder?
Was bedeutet das „1+i“? Und was bekommst du als monatlichen Zinssatz raus?
i ist der monatliche Zinssatz
1,0938 hoch1/12 = (1+i)
1,0075 = (1+i)
i = 0,075 oder 7,75 %
Nein, i müsste doch dann 0,75% sein, oder? Weil oben steht ja 1,0075 = (1+i).
stimmt, wollte ich gerade berichtigen. i = 0,0075 oder 0,75%
Das heißt, monatlich müsste es dann eine Belastung von 833,33 EUR plus die Zinsen also insgesamt 839,58 EUR sein, oder?
???
Hatte ich doch oben geschrieben. Jetzt musst du die rentenbarwertformel nehmen, um die monatl. annuität auszurechnen.
Rentenbarwert (200.000) = rentenbarwertfaktor * Annuität
Rentenbarwertfaktor (RBF) = (1-qhoch-t)/ i mit q = 1+i
Wir haben ja jetzt den monatlichen Zinsfaktor schon ausgerechnet und haben auch die Laufzeit von 20 Jahren. Müsste die Annuität dann nicht entsprechend 20 * 12 = 240 sein?
RBF = (1-qhoch-t)/ i mit q = 1+i ; t =240 ; i = 0,0075
RBF = 111,14
200.000 = 111,14 * annuität
monatliche annuität = 1799 Euro
Und diese monatliche Annuität wäre dann die gesamte monatliche Belastung für den Käufer?
Ja, annuitaet ist die monatliche Rate bestehend aus Zins und Tilgung.
Easy: Gar nicht.
Ein solcher Zinssatz würde heutzutage bei einer Immobilienfinanzierung als Wucher gelten, wäre daher illegal und der Vertrag ungütig.
Ja, mit Stift und Papier.