Wahrscheinlichkeitsrechnung, 3 Ampeln, Wahrscheinlichkeit, dass exakt 2 mal rot angezeigt wird?

2/3 hoch 2 mal 1/3 mal 3. 2/3 ist die wahr. das ampel rot ist 1/3 das gegenereignis und das mal 3 da es an allen 3 stellen passieren kann

Einfach addieren. Jeder deiner Einzelfälle hat die Wahrscheinlichkeit von 1/8. Drei richtige Möglichkeiten gibt es. 5 falsche Möglichkeiten gibt es. Die Gesamtwahrscheinlichkeit ist immer 1, also für die falschen und richtigen Möglichkeiten zusammen. In deinem Fall also 1/8 + 1/8 + 1/8 = 3/8 = 0,375.

Es könnte aber auch sein, dass die Ampeln gelb anzeigen. Ist daran in der Aufgabenstellung auch gedacht worden? Und außerdem geht die Idee, dass rot und grün gleichwahrscheinlich sind ja davon aus, dass beide Anzeigedauern gleich lang sind. Sonst stimmt das auch nicht.

Aber vereinfacht ist das so erstmal ok.

Das kannst Du auch ganz exakt über die Binomialverteilung machen. Also (n über k) * p^k * (1-p)^(n-k). Wobei n = 3 Ampeln insgesamt, k = 2 rote Ampeln, p = 0,5 (Warscheinlichkeit für Rot an einer Ampel, wobei das nur geschätzt ist, da die Phasen unterschiedlich lang sein können). Das ^ heißt hoch.

Die richtige Lösung wurde ja schon genannt. Ei guter Lösungsweg für Wahrscheinlichkeitsprobleme sind der Baum oder die Tabelle. Ein Beispiel dazu in der Anlage.

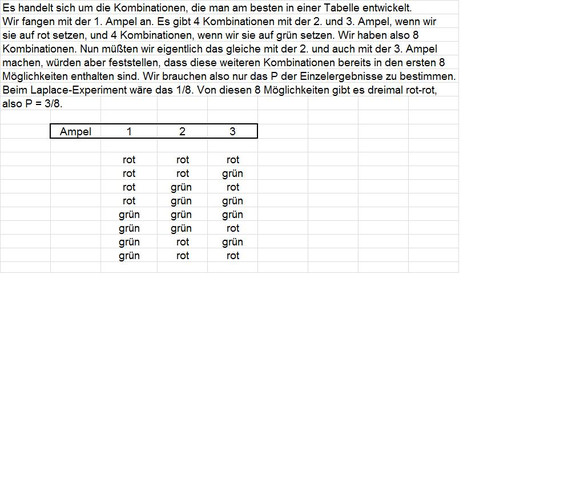
2. Teil der Pfadregel!