Sudoku raten
Kann es bei einem Sudoku vorkommen, dass man eine Zahl schlichtweg raten muss, da es auf keinem Feld eindeutig ist, welche Zahl hinkommt?
7 Antworten
Genau wie claushilbig sagt: Es gibt (ganz selten) welche mit 2 Lösungen, wo die meisten Felder zwar übeeinstimmen, aber die übrigen paarweise vertauscht sind. Die Sudokus sind heute alle computergeneriert, aber manchmal fehlt offenbar ein Prüfprogramm, das auf Doppeldeutigkeit prüft.
nope. du musst bei gewissen schwierigkeitsgrad ein paar mal um die ecke denken. es gibt immer einen weg.
liebe Grüße
Das ist dann ein unterbestimmtes Sudoku, eigentlich also ein Fehler des Erstellers.
Es gibt 3 Arten von SUDOKU-Starteinstellungen:
A) nur eine Lösung = eindeutig lösbar
B) mehrdeutige Lösung
C) keine Lösung (Ersteller hat grobe Fehler begangen)
Je weniger Anfangsziffern gegeben sind, um so höher ist die Wahrscheinlichkeit einer Mehrdeutigen Lösung!
Die kleinste bisher gefundene Start-Zahl für eine eindeutige Lösung ist angeblich 17.
Zählt man nur die Sudokus, die zusätzlich auch unter Drehungen oder Spiegelungen verschieden sind, so verbleiben nur noch 5472730538 (5,5 Milliarden) verschiedene Sudokus (Ed Russell und Frazer Jarvis 2006).
Mindestanzahl der vorgegebenen Felder zu bestimmen, damit ein Sudoku lösbar ist, ist ein noch ungelöstes mathematisches Problem.
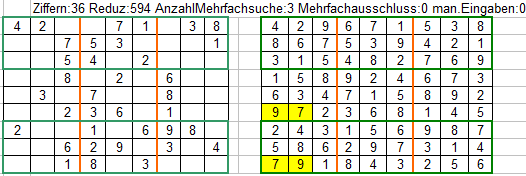
Hier 2 Beispiele für Mehrfachlösungen:
Bild 1: 7 und 9 können vertauscht werden, weil Summe dadurch nicht verändert wird
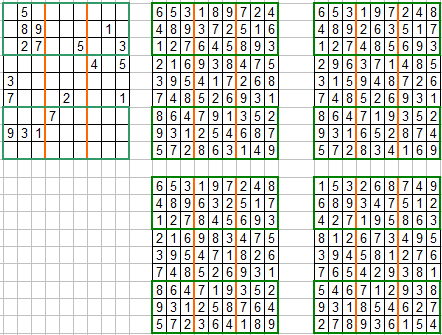
Bild2: zig Mehrfachlösungen
Man kann sich das unter einen (Logik-)Pfad vorstellen, wo sich der Weg in 2 mögliche andere (Lösungs-)Wege aufspaltet.
Bei eindeutigen Lösungen muss man nicht raten, da es wie eine exakte Gleichung lösbar ist.
Ein Schachcomputer rechnet jeden möglichen Zug bis zum Ende der Partie durch Matt. Er rät also und probiert aus.
So gesehen ist "raten" bei schweren Sudokus durchaus innerhalb eines mathematisch korrekten Lösungsweges. Man kann also durchaus Sudokus konstruieren, wo manchmal keine der "normalen" Methoden weiterhilft; oder diese - z.B. 7er-Zahlenpaarungen - einfach undurchschaubar werden.
Ich habe etwas im Kopf, dass ein Sudoku mit 11 Zahlen formal eindeutig bestimmt ist, d.h. wenn du eine hinreichend komplexes Gleichungsystem verwendest .
Ich weiß aber nicht, ob für diese 11 Zahlen irgendwelche besonderen Bedingungen gelten müssen, und bin auch nicht mehr sicher, ob das nur eine Vermutung war, oder diese inzwischen (elegant oder mit erheblichem "brute-and-force"-Anteil) bewiesen ist.
Praktisch gehe ich so vor, dass ich zuweilen für eine geratene Zahl eine der (durchnummeriert gedachten) Buchstaben a bis i verwende, und ebenso für alle später erschlossenen. Wenn ich dann auf einen Widerspruch stoße, war das falsch geraten; ich lösche die auf der Hypothese beruhenden Zahlen wieder (nicht aber die als Ziffern geschriebenen) und wähle statt der ersten geratenen die Alternative (die dann als Ziffern geschrieben wird) oder aber eine Alternative (die dann wieder als Buchstabe geschrieben wird).
Stimmt leider nicht, ich hatte schon mehrfach Sodokus, die keine eindeutige Lösung hatten, bei denen man z. B: Zahlen paarweise vertauschen konnte.